算法的渐进时间复杂度 简称时间复杂度
在常数操作数量的表达式中,
只要高阶项,不要低阶项,也不要高阶项的系数,剩下的部分
如果记为f(N),那么时间复杂度为O(f(N))
简单来说就是大O表示法不考虑乘以、除以、加上、减去的数字
如O(n+26)、O(n-26)、O(n*26)、O(n/26)都可以表示为O(n)
O(an^2+bn+c)表示为O(n^2) 不考虑常数项 不考虑低阶项
评价一个算法流程的好坏,先看时间复杂度的指标,然后再分
析不同数据样本下的实际运行时间,也就是常数项时间(就是系数)。
大O表示法指出了算法有多快
大O表示法指出了最糟情况下的运行时间
算法的速度指的并非时间,而是操作数的增速
谈论算法的速度时,我们说的是随着出入的增加,其运行时间将以怎么样的速度增加
Demo1
如遍历输出一个数组 O(n)
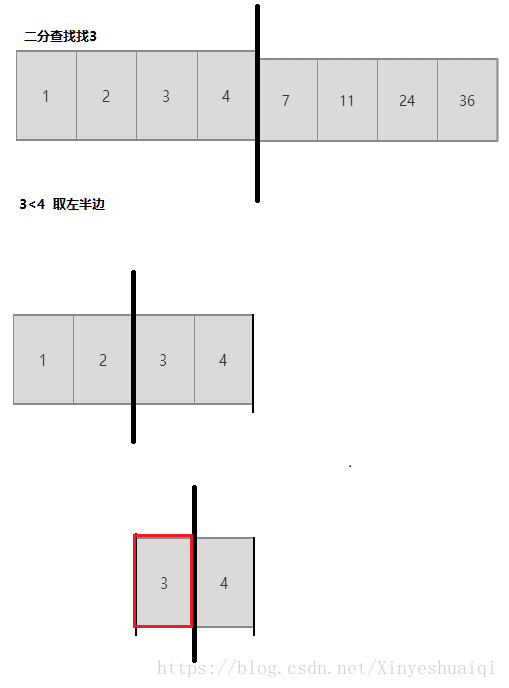
如二分查找 O(log n) log n默认是以2为底的 (在有序数组中每次取原来的一半,8个数就需要二分3次)
Demo2

绘制上述16个小方格
法一: 一个个画,画16个 O(n)
法二:依次对折,只用对折4次就能形成16个小方格 O(logn)
Demo3

流程1: O(M*N)
流程2: O(M*logN)
流程3: 类似外排的方法
1)排序 O(MlogM)
2) O(N+M)
总的复杂度: O(MlogM)+ O(N+M) 因为N和M的大小不能确定,不能判断MlogM和N的大小
流程2和3的选取根据样本量的多少决定(根究N和M的大小)
附上流程3代码:
public static void solution(int []A ,int[]B){
int N=A.length;
int M=B.length;
//先把M排序 快速排序的复杂度为 O(MlogM)
quicksort(B,0,M-1);
int i=0;
int j=0;
while(i<N && j<M){
if(B[j]<A[i]){
System.out.println(B[j]);
j++;
}else if(B[j]==A[i]){
//do nothing
j++;
}
else if(B[j]>A[i]){
//do nothing
i++;
}
}
}
public static int partition(int []a,int low,int high){ //核心算法在分区,利用递归不断缩小分区的区间,最终达到排序的目的
int i=low;
int j=high;
int pivotkey=a[low];
while(i<j){
while(i<j&&a[j]>=pivotkey){
j--;
}
a[i]=a[j]; //a[j]<pivotkey
while(i<j&&a[i]<=pivotkey){
i++;
}
a[j]=a[i]; //a[j]>pivotkey
}
a[i]=pivotkey; //基准归位
return i;
}
public static void quicksort(int []a,int low,int high){
if(low<high){
int pivotkeyLocation=partition(a,low,high); //找到中轴
quicksort(a,low,pivotkeyLocation-1); //对中轴左边的排序
quicksort(a,pivotkeyLocation+1,high); //对中轴右边的排序
}
else {
return;
}
}
public static void main(String []args){
int []A={2,4,7,8,9}; //有序数组
int []B={1,9,7,8,4,5,6};
solution(A,B);
}
运行结果

算法的存储空间需求:
空间复杂度 算法所需存储空间的度量 额外的的存储空间
如创建一个临时变量
如创建一个数组 ,或创建一个HashMap
都是算法消耗的额外存储空间
转载请注明:汪明鑫的个人博客 » 算法回马枪 算法复杂度

说点什么
您将是第一位评论人!