目录
前言
任何数据结构都是由数组和链表组成
包括树、图、跳表等等,万变不离其宗
本文主要是对图相关内容进行复习和整理
树图这些玩意在大学都是老大难的一块
图的定义
图(Graph)是由顶点和连接顶点的边构成的离散结构
图是很灵活的一种数据结构
在某种意义上树和链表也是特殊的图
图的分类
- 有向图
- 无向图
- 带权图
图的存储
- 邻接矩阵
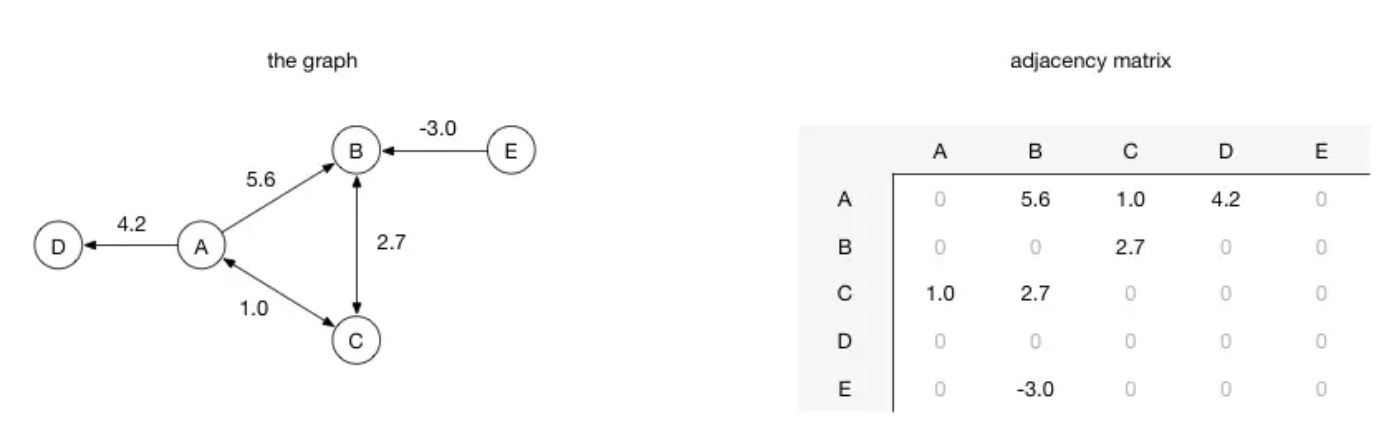
- 邻接表
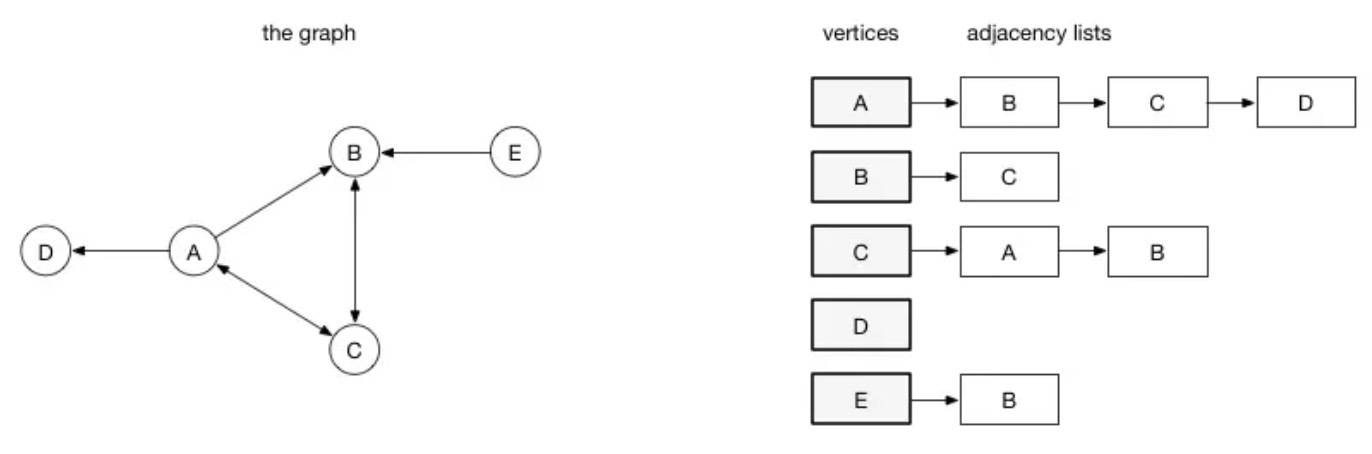
一个大型的社交网络选择哪种存储方式呢?
临接表,因为矩阵太占内存资源,比如有2亿个用户,2亿用户间的关系用图表示,是一个稀疏图
很多用户之间并没有关系,也要表示在矩阵里
因此使用临接表更合适,虽然存在链表的遍历,但总比2亿 * 2亿的矩阵更好吧
广度优先与深度优先搜索
图常常用来搜索一个顶点到另一个顶点的最短路径
由此衍生了很多算法
本文只简单高下广度优先和深度优先算法
因为算法水平着实垃圾,这两个都看了好久,嘛的
我们统一使用邻接表
public class Graph { // 无向图
private int v; // 顶点的个数
private LinkedList<Integer> adj[]; // 邻接表
public Graph(int v) {
//初始化临接表
this.v = v;
adj = new LinkedList[v];
for (int i=0; i<v; ++i) {
adj[i] = new LinkedList<>();
}
}
public void addEdge(int s, int t) { // 无向图一条边存两次
adj[s].add(t);
adj[t].add(s);
}
}
广度优先
顾名思义,地毯式搜索,优先搜索距离出发地最近的点,慢慢扫秒式的向外扩散
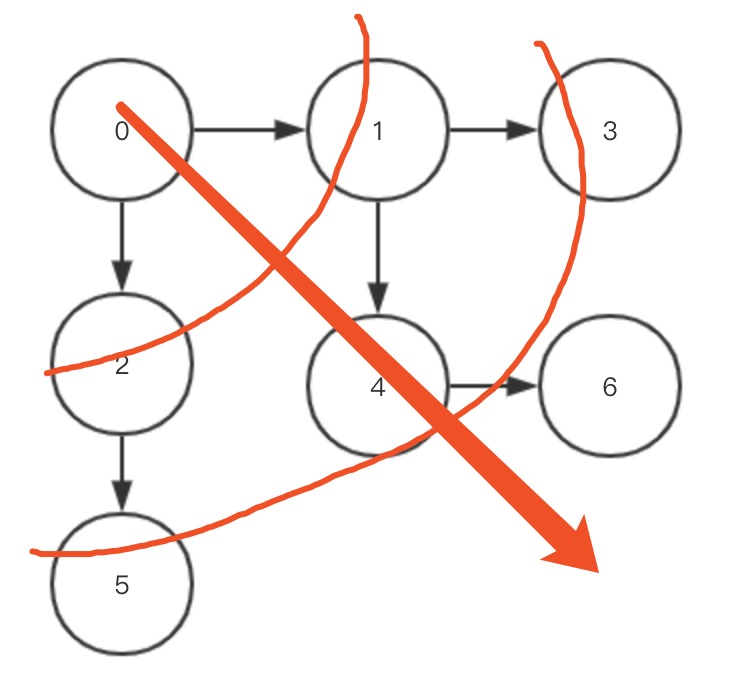
s表示起始顶点, t表示终止顶点。搜索一条从s到t的路径
借助队列来实现,每次出队列,就把当前顶点的邻接点全部依次入队列
queuevisited 表示顶点是否已遍历prev 表示当前顶点的前一个顶点,比如上图:prev(4) = 1public void bfs(int s, int t) {
if (s == t) return;
//顶点个数
boolean[] visited = new boolean[v];
visited[s]=true;
Queue<Integer> queue = new LinkedList<>();
queue.add(s);
int[] prev = new int[v];
//最初前一个节点都是-1
for (int i = 0; i < v; ++i) {
prev[i] = -1;
}
//循环终止条件:队列为空
while (queue.size() != 0) {
//出队列
int w = queue.poll();
//找到w的临接点
for (int i = 0; i < adj[w].size(); ++i) {
int q = adj[w].get(i);
//没有被遍历过,入队列
if (!visited[q]) {
//置当前顶点前置节点为w
prev[q] = w;
//找到目标顶点
if (q == t) {
print(prev, s, t);
return;
}
//顶点q置为已遍历
visited[q] = true;
//入队列
queue.add(q);
}
}
}
}
// 递归打印s->t的路径
private void print(int[] prev, int s, int t) {
if (prev[t] != -1 && t != s) {
print(prev, s, prev[t]);
}
System.out.print(t + " ");
}
深度优先
走迷宫式,一直往里走,走到头再回头换条路走
boolean found = false;
public void dfs(int s, int t) {
found = false;
boolean[] visited = new boolean[v];
int[] prev = new int[v];
for (int i = 0; i < v; ++i) {
prev[i] = -1;
}
recurDfs(s, t, visited, prev);
print(prev, s, t);
}
private void recurDfs(int w, int t, boolean[] visited, int[] prev) {
if (found == true) return;
visited[w] = true;
if (w == t) {
found = true;
return;
}
for (int i = 0; i < adj[w].size(); ++i) {
int q = adj[w].get(i);
if (!visited[q]) {
prev[q] = w;
//深度搜索
recurDfs(q, t, visited, prev);
}
}
}
应用场景
图可以表示一个庞大的社交网络
地铁/公交/路线等等
状态机
搜索任务


说点什么
您将是第一位评论人!