目录
冒泡排序
/*
* 冒泡排序
*
* 每一趟出来一个最大的数(冒出一个泡泡)
*
* */
public class BubbleSort {
public static void bubbleSort(int []arr){
//首先对输入做判断
if(arr==null||arr.length<2){
return;
}
for(int i=0;i<arr.length-1;i++){ //一共n-1躺排序(n个数需要n-1躺排序) 每一趟冒出来一个最大的数
for(int j=0;j<arr.length-1-i;j++){
//每过一趟排序,j的遍历范围缩减1 (最右边的坑已经被最大的数给占了,现在第二大的数准备入从右往左
//数的第二个坑...)
if(arr[j]>arr[j+1]){
MySwap(arr,j,j+1);
}
}
}
}
public static void MySwap(int []arr ,int i,int j){
int temp=arr[i];
arr[i]=arr[j];
arr[j]=temp;
}
public static void main(String []args){
int []arr={2,0,4,8,9,1,2,7};
bubbleSort(arr);
for (int i = 0; i <arr.length ; i++) {
System.out.println(arr[i]);
}
}
}
时间复杂度: O(n^2)
空间复杂度: O(1)
冒泡排序是稳定的排序
选择排序
/*
* 选择排序 每次都选择一个最小的
* */
public class SelectSort {
public static void selectSort(int []arr){
for(int i=0;i<arr.length;i++){ //i来控制遍历的范围 在该范围下选择一个最小的数
int minIndex=i;
for (int j = i+1; j < arr.length; j++) { //找出一个最小的数放在minInde的位置上
if(arr[j]<arr[minIndex]){
MySwap(arr,minIndex,j); //这样写是有问题的
}
}
}
}
//优化版 遍历完所有数,确定minindex 在Swap
public static void selectSort_edition2(int []arr){
for(int i=0;i<arr.length;i++){ //i来控制遍历的范围 在该范围下选择一个最小的数
int minIndex=i;
for (int j = i+1; j < arr.length; j++) { //找出一个最小的数放在minIndex的位置上
if(arr[j]<arr[minIndex]){
minIndex=j;
}
}
MySwap(arr,i,minIndex); //确定一个最小的只交换一次
}
}
public static void MySwap(int []arr ,int i,int j){
int temp=arr[i];
arr[i]=arr[j];
arr[j]=temp;
}
public static void main(String []args){
int []arr={2,0,42,8,9,11,2,7};
selectSort_edition2(arr);
for (int i = 0; i <arr.length ; i++) {
System.out.println(arr[i]);
}
}
}
时间复杂度: O(n^2)
选择排序不是稳定的排序
插入排序
斗地主
类似你手里的牌是已经排好序的,你新起一张牌,这张牌与你手里的最大的一张牌比较,如果大,就放你右边,如果小,就和手里最大的牌之前的一张牌比较…
根据当前的大小能比较到哪个位置,插入
/*
插入排序
* */
public class InsertSort {
public static void insertSort(int []arr){
for (int i = 1; i < arr.length; i++) { //考虑的当前数i 往前面有序区插入(0 到 i-1)
for (int j = i-1; j >=0 ; j--) { //位置i的前一个数
if(arr[j]>arr[j+1]){
MySwap(arr,j,j+1);
}
}
}
}
//添加标记
public static void insertSort_edition2(int []arr){
boolean isSwaped =false; //i和i-1是否交换了 如果没有交换直接break
for (int i = 1; i < arr.length; i++) { //考虑的当前数i 往前面有序区插入(0 到 i-1)
for (int j = i-1; j >=0 ; j--) { //位置i的前一个数
if(arr[j]>arr[j+1]){
MySwap(arr,j,j+1);
isSwaped=true;
}
if(!isSwaped){
break;
}
}
}
}
public static void MySwap(int []arr ,int i,int j){
int temp=arr[i];
arr[i]=arr[j];
arr[j]=temp;
}
public static void main(String []args){
int []arr={2,0,42,8,9,11,2,7};
insertSort_edition2(arr);
for (int i = 0; i <arr.length ; i++) {
System.out.println(arr[i]);
}
}
}
注意:选择排序和冒泡排序跟数据状况是没有关系的 严格的 O(n^2)
插入排序的好坏要根据数据状况决定的
如果已经排好序了,插入排序O(n)
如果是逆序,插入排序O(n^2)
于是有了最好情况,最差情况
这样的算法按照最差的情况估计算法复杂度,因此插入排序就是O(n^2)
插入排序是稳定的排序
快速排序
public static int partition(int []a,int low,int high){ //核心算法在分区,利用递归不断缩小分区的区间,最终达到排序的目的
int i=low;
int j=high;
int pivotkey=a[low];
while(i<j){
while(i<j&&a[j]>=pivotkey){
j--;
}
a[i]=a[j]; //a[j]<pivotkey
while(i<j&&a[i]<=pivotkey){
i++;
}
a[j]=a[i]; //a[j]>pivotkey
}
a[i]=pivotkey; //基准归位
return i;
}
public static void quicksort(int []a,int low,int high){
if(low<high){
int pivotkeyLocation=partition(a,low,high); //找到中轴
quicksort(a,low,pivotkeyLocation-1); //对中轴左边的排序
quicksort(a,pivotkeyLocation+1,high); //对中轴右边的排序
}
else {
return;
}
}存在的问题:
1)一次只能处理一个基准,但数组中可能存在多个数和基准相等,影响效率,有没有办法让等于基准的数不再重复排序?
2)每次取一个第一个\最后一个为基准,但可能是小于区域或大于区域太大,影响算法效率,因此随机取一个数为基准
快速排序改进的的分区思想参考 : 荷兰国旗
改进的随机快排
public static void quicksort(int[] a, int low, int high) {
if (low< high) {
swap(a, low + (int) (Math.random() * (high - low + 1)), high); //low到high间随机选择一个位置 与 high交换位置
int[] p = partition(a, low, high);
quicksort(a, low, p[0]);
quicksort(a, p[1] , high);
}
}
public static int[] partition(int[] a, int low, int high) {
int n=a[high]; //取为标准
int i = low - 1; //小于n的区域指针
int j = high+1; //大于n的区域指针
int temp =low; //遍历指针
while (temp < j) {
if(a[temp]<n){
i++; //小于n的区域的边界指针+1;
swap(a,i,temp);
temp++; //temp指针后移
}
else if (a[temp] == n){
temp++; //temp指针后移
}
else{ //a[temp] > n
j--; //大于n的区域的边界指针-1;
swap(a,temp,j);
}
}
return new int[] { i, j}; //返回一个数组 只有两个元素分别记录小于区域的边界和大于区域的边界
}
public static void swap(int[] a, int i, int j) {
int temp = a[i];
a[i] = a[j];
a[j] = temp;
}
public static void main(String[] args) {
int a[] ={1,2,5,1,13,5,7,6,22,2};
quicksort(a,0,a.length-1);
for(int n:a){
System.out.print(n+" ");
}
}时间复杂度 O(nlogn)
快速排序不是稳定的排序,但也可以实现稳定,比较难
归并排序

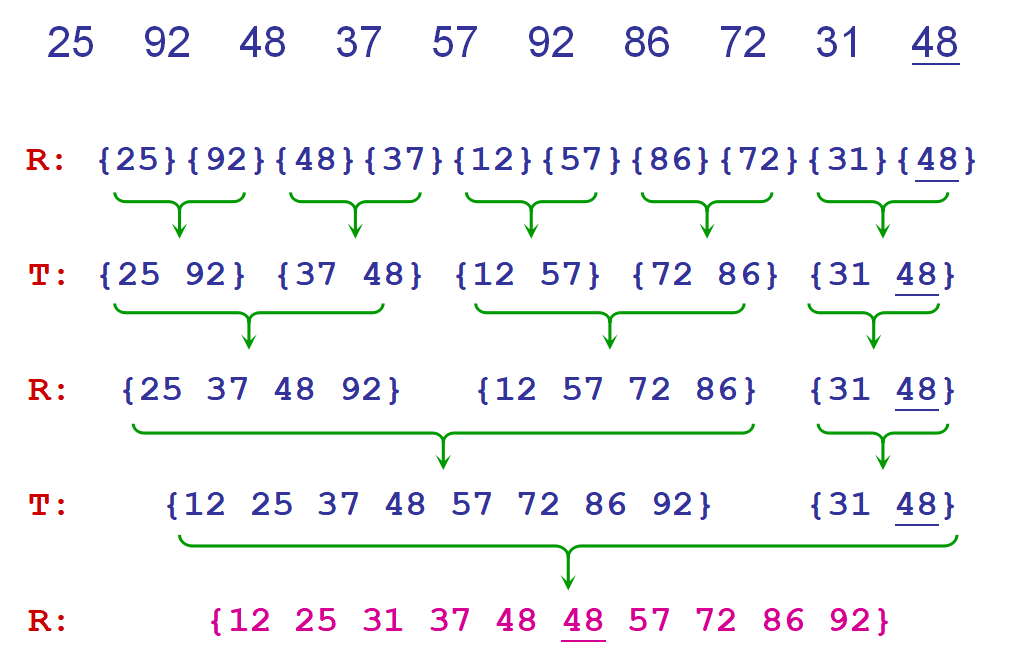
public static void mergeSort(int[] arr, int l, int r) {
if (l == r) { //递归终止条件,分到只有一个数
return;
}
int mid = (l+r)/2; //分而治之
mergeSort(arr, l, mid);
mergeSort(arr, mid + 1, r);
merge(arr, l, mid, r); //把两个有序的数组合并成一个有序的数组
}
public static void merge(int[] arr, int l, int m, int r) {
int[] help = new int[r - l + 1]; //辅助数组
int i = 0;
int p1 = l;
int p2 = m + 1;
while (p1 <= m && p2 <= r) {
help[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++];
}
while (p1 <= m) {
help[i++] = arr[p1++];
}
while (p2 <= r) {
help[i++] = arr[p2++];
}
for (i = 0; i < help.length; i++) {
arr[l + i] = help[i];
}
}归并排序是稳定的排序
时间复杂度为 O(nlogn)
堆排序
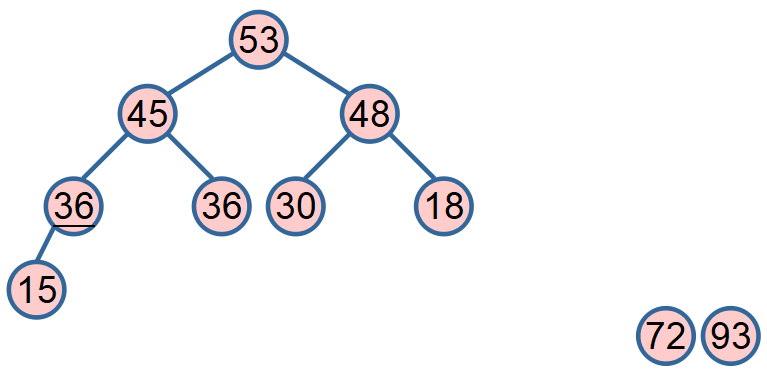
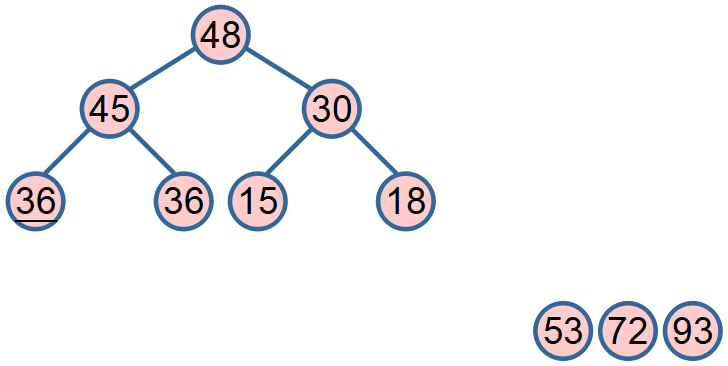
用建堆的方法来选择待排序区间的最大或最小键值。
堆就是一个完全二叉树
完全二叉树补全就是满二叉树
这棵完全二叉树上每个结点的值比左孩子和右孩子值都要大(大根堆), 或比左孩子和右孩子值都要小(小根堆)。
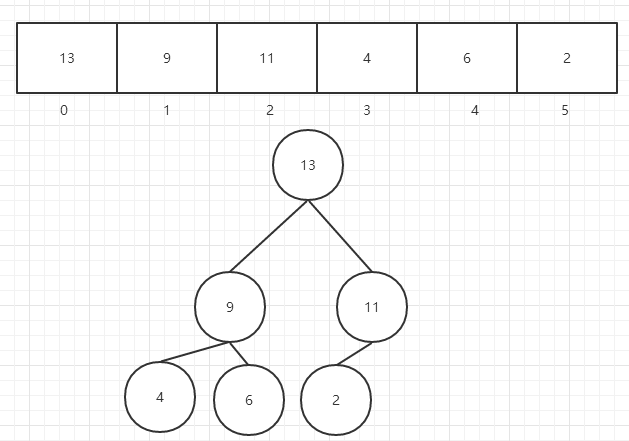
数组和二叉树是对应的
假设i为当前节点的位置
左子节点下标=2*i+1
右子节点下标=2*i+2
父节点下标=(i-1)/2
堆排序不是稳定的排序

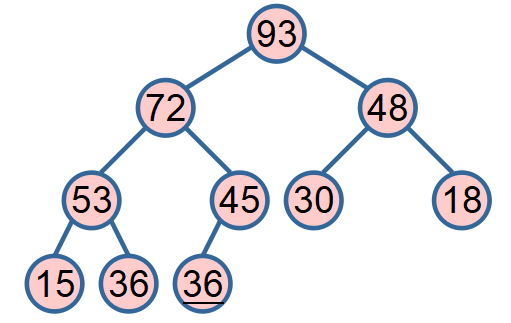
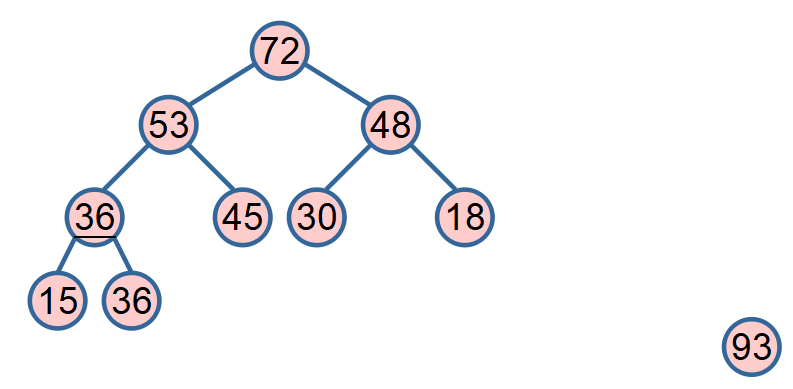
public static void heapSort(int[] a) {
if (a == null || a.length < 2) {
return;
}
for (int i = 0; i < a.length; i++) { //大根堆形成但可能无序
heapInsert(a, i);
}
int size = a.length;
swap(a, 0, --size); //把最后一个位置和堆顶交换 意思是每次把最大值放在最后面,然后缩小堆的范围
while (size > 0) {
heapify(a, 0, size); //可能小的数到堆顶,整个堆需要做一次调整modify,又形成大根堆
swap(a, 0, --size);
}
}
public static void heapInsert(int[] a, int index) {
while (a[index] > a[(index - 1) / 2]) { //比较当前节点与其父节点的大小
swap(a, index, (index - 1) / 2);
index = (index - 1) / 2;
}
}
public static void heapify(int[] a, int index, int size) {
int left = index * 2 + 1;
while (left < size) {
int largest = left + 1 < size && a[left + 1] > a[left] ? left + 1 : left; //得到较大节点位置
largest = a[largest] > a[index] ? largest : index;
if (largest == index) {
break;
}
swap(a, largest, index);
index = largest;
left = index * 2 + 1;
}
}
public static void swap(int[] a, int i, int j) {
int temp = a[i];
a[i] = a[j];
a[j] = temp;
}
public static void main(String[] args) {
int a[] ={1,2,5,1,13,5,7,6,22,2};
heapSort(a);
for(int n:a){
System.out.print(n+" ");
}
}
桶排序
非基于比较的排序
public static void bucketSort(int[] a) {
int max = -1;
for (int i = 0; i < a.length; i++) {
max = Math.max(max, a[i]);
}
int[] bucket = new int[max + 1]; //需要准备max+1个桶来装数 比如最大值是6,你需要装0,1,2,3,4,5,6这7个数的桶
for (int i = 0; i < a.length; i++) {
bucket[a[i]]++;
}
//根据堆重新给数组赋值
int index = 0;
for (int j = 0; j < bucket.length; j++) {
while (bucket[j]> 0) {
a[index] = j;
index++;
bucket[j]--; //桶值减1,当为0时,遍历下一个桶
}
}
}
public static void main(String[] args) {
int a[] ={1,2,5,1,13,5,7,6,22,2};
bucketSort(a);
for(int n:a){
System.out.print(n+" ");
}
}

说点什么
您将是第一位评论人!