每周一练（2） – 汪明鑫的个人博客

算法老大难：各种树 + 递归 + 动态规划

今天简单复习和练习下递归，

每周一练【算法 + SQL + JAVA API】预计持续一年【19年年底-20年年底】，所以难度会由易到难，前面比较简单，大佬请跳过该系列

写一个简单的走楼梯的例子，相信大家都做过

从1楼走到n楼,一次要么走1层，要么走2层，一共有多少种走法？

package pers.wmx.practice.digui;

/**
 * 走楼梯要么走一层，要么走两层
 * 一共走floor层有多少种方法？
 *
 * @author wmx
 * @date 2019-12-06
 */
public class LadderTest {
    //floor 表示走完多少层
    public static int ways(int floor){
        if(floor == 1){
            return 1;
        }

        if(floor == 2){
            return 2;
        }

        return ways(floor-1) + ways(floor-2);
    }

    public static void main(String[] args) {
        System.out.println(ways(1));
        System.out.println(ways(2));
        System.out.println(ways(3));
        System.out.println(ways(4));
        System.out.println(ways(5));
        System.out.println(ways(6));
    }

}

学习递归最大的误区是妄想考虑所有的情况，一层层往下想，这样就会造成死循环

递归举实际的数据例子，可以帮你更好的理清，但不要一层层往下想每一个步骤，那就完了

关键在于得到一个【递归公式】和【终止条件】，缺一不可

屏蔽递归细节，我们理解是子问题已经是得到解的，问题的解是由子问题的解得到的

所以才有了上面的ways(floor-1) + ways(floor-2)

即 f(n) = f(n-1) + f(n-2) ,由子问题的答案组成，理解子问题已经得到解，

这样想就可以避免你一层层去想每一层的递归细节

当然有时你需要画一个递归树帮你理理思路也是可行的

再来个斐波那伽数列的例子：

package pers.wmx.demo;

import org.junit.jupiter.api.Test;

import java.util.Arrays;

/**
 * 斐波那契数列  f(n) = f(n-1)+f(n-2)
 *
 * 斐波那契数列是根据兔子的繁殖得到的一组数列：
 * 1, 1, 2, 3, 5, 8, 13, 21, 34, 55,89, 144, 233....
 * 其特点是从第三项开始每一项都等于前两项之和。
 *
 * @author: wangmingxin1
 * @create: 2018-10-26 10:42
 **/
public class FibonacciSequence {

    //递归法
    public static int fib1(int n){
        if(n<=0) {
            return 0;
        }
        if (n ==1) {
            return 1;
        }
        return fib1(n-1) + fib1(n-2);
    }

    //非递归   消除重复计算
    public static int fib2(int n)
    {
        int []fib=new int[50];
        fib[0]=1;
        fib[1]=1;
        for(int i=2;i<=n;i++)
        {
            fib[i]=fib[i-1]+fib[i-2];
        }
        return fib[n];
    }


    //记忆搜索法
    public static int fib3(int n)
    {
        int[] record = new int[n+1];
        Arrays.fill(record,-1);
        return fib(n,record);
    }

    private static int fib(int n, int[] record) {
       if(n==0){
           return 0;
       }
       if(n==1){
           return 1;
       }

       if(record[n]!=-1){
           return record[n];
       }

        for (int i = 2; i < n+1 ; i++) {
            record[i] = fib(i - 1, record) + fib(i - 2, record);
        }

        return record[n];

    }

    @Test
    public void test(){
        System.out.println(fib3(0));
        System.out.println(fib3(1));
        System.out.println(fib3(2));
        System.out.println(fib3(3));
        System.out.println(fib3(4));
        System.out.println(fib3(5));
    }
}

可以使用一个数组记录递归中产生的中间值（重复使用）

可提升递归算法的性能

附加一个小SQL题：

176. 第二高的薪水

编写一个 SQL 查询，获取 Employee 表中第二高的薪水（Salary） 。

+----+--------+
| Id | Salary |
+----+--------+
| 1  | 100    |
| 2  | 200    |
| 3  | 300    |
+----+--------+
例如上述 Employee 表，SQL查询应该返回 200 作为第二高的薪水。如果不存在第二高的薪水，那么查询应返回 null。

+---------------------+
| SecondHighestSalary |
+---------------------+
| 200                 |
+---------------------+

select Salary as SecondHighestSalary 
from Employee 
order by Salary desc
limit 1,1

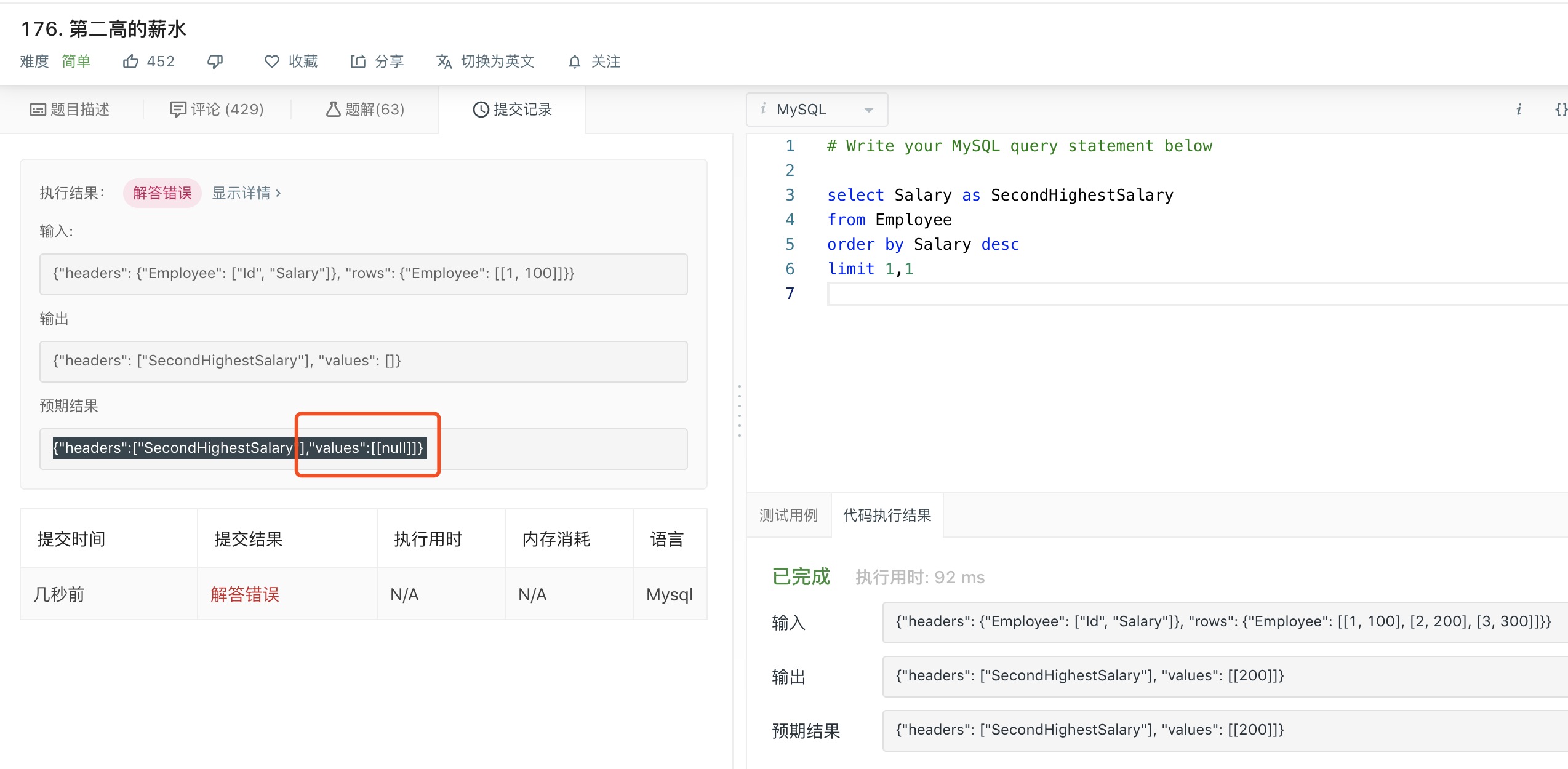
不存在第二高的薪水要求返回null。。。

这样写不符合

select max(Salary) as SecondHighestSalary  
from Employee 
where Salary< (select max(Salary) from Employee);

聚合函数得到的值为空时，返回值为“null”

转载请注明：汪明鑫的个人博客 » 每周一练（2）

176. 第二高的薪水

说点什么